Watershed by Flooding: Applied Data Structures

I’m applying some methods developed in this paper for testing purposes in my own thesis research. Specifically, I have some float-valued data, $F$, that varies along the cortical surface of the brain. Visually, I can see that there are areas where these scalar maps change abruplty. I want to identify this boundary(s) – eventually, I’ll segment out the regions I’m interested in.

Computing the Gradient Map

The authors use some conventional brain imaging software to compute the gradient of their data. The domain of this data is a triangulated mesh, described by the graph $G = (V, E)$, where $V$ are vertices in Euclidean space and $E$ the edges between these vertices. In short, for a vertex, $v_{i}$, we first need to compute the gradient vector of the scalar field at $v_{i}$. We “unfold” the 3D positions of adjacent vertices onto the tangent plane of $v_{i}$ – which we can do by orthogonally projecting the adjacent vertices onto the affine subspace at $v_{i}$ and then weighting appropriately. We then regress the graph signal (our scalar field) onto these unfolded positions. The $L_{2}$ norm of this vector is the gradient at $v_{i}$.

For each vertex, we have a normal vector to the surface $N$, its spatial 3D coordinates $v_{i} = (x, y, z)$, and a list of its adjacent vertices. We can compute the orthogonal projector onto affine subspace spanned by $N$, $P_{N}$, and it’s orthogonal complement, $Q_{N}$, as:

$$\begin{align} P_{N} &= N(N^{T}N)^{-1}N^{T} \\
Q_{N} &= I - P_{N} \end{align}$$

For any vertex, $v_{j}$, we can compute the orthogonal projection onto the affine subspace spanned by $Q_{N}$ as:

$$\begin{align} q(v_{j}) = Q_{N}(v_{j} - v_{i}) + v_{i} \end{align}$$

We generate the vectors

$$ S_{i} = f(i) - \begin{bmatrix} f(v_{1}) \\
f(v_{2}) \\
\vdots \\
f(v_{j}) \end{bmatrix} \in \mathbb{R}^{j} \;\;\; R_{i} = \begin{bmatrix} q(v_{1}) \\
q(v_{2}) \\
\vdots \\
q(v_{j}) \end{bmatrix} \in \mathbb{R}^{j \times 3} $$

where $S_{i}$ is the difference between the scalar value at our vertex $f(v_{i})$ and the vector of adjacent $j$ scalar field values, and $R_{i}$ is the matrix of $j$ orthogonally projected adjacent vertex coordinates. Then we perform least squares regression to solve for $\beta$:

$$\begin{align} S_{i} = R_{i}\beta \end{align}$$

where $\beta \in \mathbb{R}^{3}$, which indicates how much each coordinate axis contributes to variation in the scalar field at $v_{i}$. The gradient value at vertex $v_{i} = \left || \beta \right||_{2}$.

Watershed By Flooding Algorithm

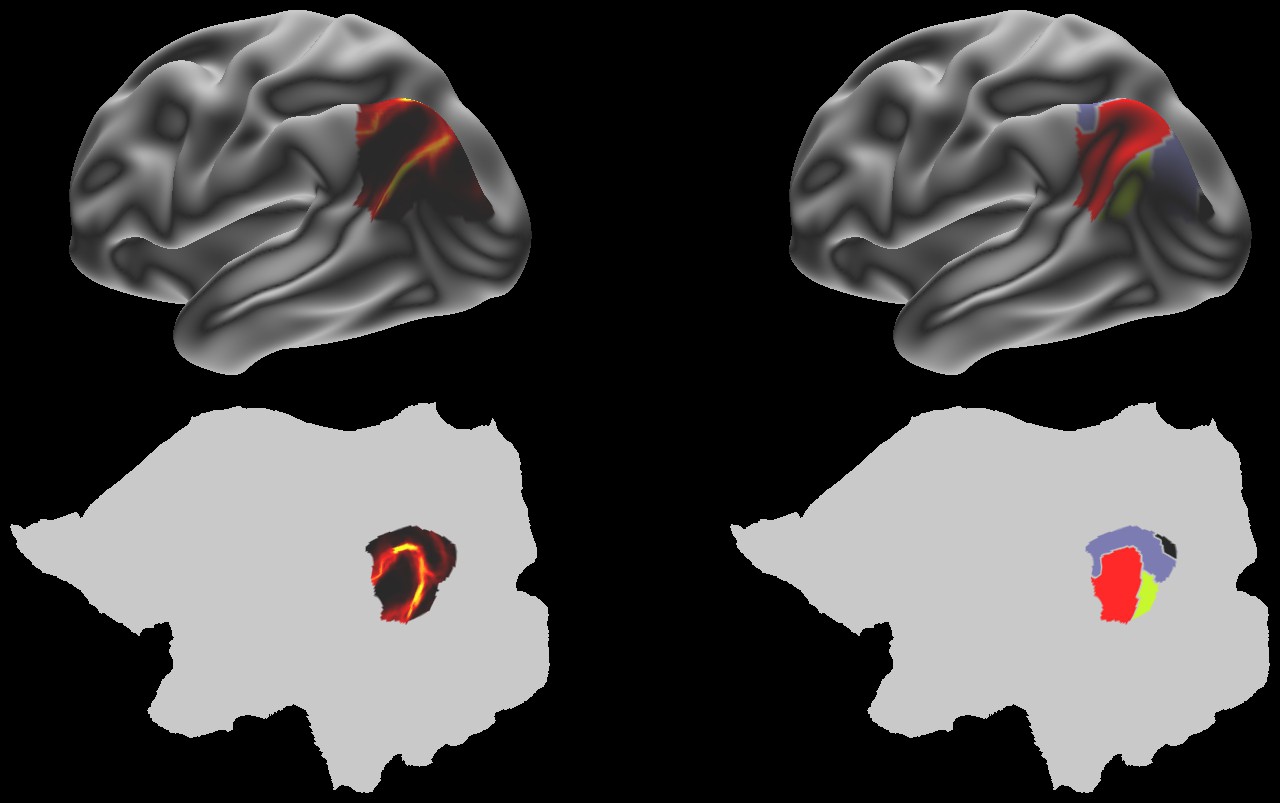
The new scalar field of $L_{2}$ norms is our gradient field, which describes how “quickly” our original data changes at each vertex. We can now apply the Watershed Algorithm to segment our mesh data. In brief, the watershed algorithm treats the gradient field as a *topographic map*: low-elevation areas (areas with a small gradient) are “water basins”. If we imagine water flooding this map from the bottom up, basins at low elevation will flood first, while areas at higher elevations will fill last. When water basins meet, the water has reached a “boundary” (or ridgeline, if we’re using the topographic map idea).

I’ve implemented an algorithm variant called “Priority Flooding”, using Python’s heapq priority queue data type class. The priority queue is an application of the binary heap data structure – as nodes are added to the heap, the branching process determines where to put nodes (left or right of a current node), based on some value – in the case of the priority queue, this value is the “priority”. We utilize the priority queue because it gives us a principled way to iterate over unlabeled vertices, and, with some auxilliary data structures, is guaranteed to converge. The algorithm proceeds as follows:

1. Identify local minima, and assign each minima a unique label

2. Add directly adjacent vertices of local minima to priority queue (lower gradient -> higher priority)

3. While the queue is not empty, get the highest-priority item

   • If vertices adjacent to this vertex have only one label, assign this vertex to that label

   • Else assign this vertex as a boundary vertex

   • Add unlabed adjacent vertices to the queue

import numpy as np
from queue import PriorityQueue

class PriorityFlood(object):

    """
    Class to segment a scalar field using the Priority Flooding
    watershed algorithm.
    """

    def __init__(self):

        self.pq = PriorityQueue()

    def fit(self, gradient, A, M):

        """
        Fitting procedure for watershed algorithm.

        Parameters:
        - - - - -
        gradient: float, array
            map of gradient values of scalar field
        A: dict of lists
            adjacency list of data domain
        M: list
            local minima in scalar field used to seed algorithm
        """

        # initialize empty label vector
        labels = np.zeros((gradient.shape))
        labels[:] = np.nan

        # keep track of items in queue
        in_queue = np.zeros((gradient.shape)).astype(np.bool)

        # assign local minima unique labels
        # add their adjacent vertices to heap
        for i, loc_min in enumerate(M):

            # label local minima
            labels[loc_min] = i+1

            # add neighbors of local minima to p-queue
            for nidx in A[loc_min]:
                in_queue[nidx] = True
                self.pq.put((gradient[nidx], nidx))

        # iterate over p-queue items
        # items assigned to a label or
        # assigned as a boundary
        while not self.pq.empty():

            # get highest priority item
            # mark as not in p-queue
            [gr, idx] = self.pq.get()
            in_queue[idx] = False

            # get item neighbors and their labels
            i_neighbors = np.asarray(A[idx])
            i_nlabels = labels[i_neighbors]

            # get labels of adjacent vertices that are not nan
            nans = np.isnan(i_nlabels)
            unique_labels = np.unique(i_nlabels[~nans])

            # if more than one unique label
            # assign current vertex as border vertex
            if len(unique_labels) > 1:
                continue

            # otherwise assign to water basin
            else:

                # basin assignment
                labels[idx] = unique_labels

                # identify neighbors without labels that arent in the p-queue
                gidx = np.where((nans) & (~in_queue[i_neighbors]))[0]

                # add these to p-queue
                for nidx in i_neighbors[gidx]:
                    if not in_queue[nidx]:
                        in_queue[nidx] = True
                        self.pq.put((gradient[nidx], nidx))

        self.labels_ = labels

One caveat that came up is that the PriorityQueue class does not check for duplicates – that is, two vertices might share an adjacent vertex, and this vertex might have already been added to the heap. In this case, we would unnecessarily view the same vertices many times. To alleviate this, we create a boolean Numpy array, in_queue, that stores whether an item is already in the queue.